I spend a lot of time thinking about the connections between information theory and reality, and this led me to both a mathematical theory of epistemology and a completely new model of physics. I did work on related foundations of mathematics in Sweden back in 2019, but I tabled it, because the rest of the work was panning out incredibly well, and I was writing a large number of useful research notes. Frankly, I didn’t get very far in pure mathematics, other than discovering a new number related to Cantor’s infinite cardinals, which is a big deal and solves the continuum hypothesis, but short of that, I produced basically nothing useful.
Euler’s Identify is False
Recently I’ve had some more free time, and I started thinking about complex numbers again, in particular Euler’s Identity. I’m a graph theorist “by trade”, so I’m not keen on disrespecting what I believe to be a great mathematician, but Euler’s identity is just false. It asserts the following:
 .
.
I remember learning this in college and thinking it was a simply astonishing fact of mathematics, you have all these famous numbers connected through a simple equation. But iconoclast that I am, I started questioning it, specifically, setting  , which implies that,
, which implies that,
 , and therefore,
, and therefore,
 , and so
, and so  .
.
This implies that,
 , and therefore,
, and therefore,  .
.
Now typically, we assume that 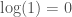 . However, applying this produces a contradiction, specifically, we find that,
. However, applying this produces a contradiction, specifically, we find that,
 , which implies that
, which implies that  , and therefore
, and therefore  .
.
This implies that  , which contradicts the assumption that
, which contradicts the assumption that 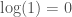 . That is, the exponent of
. That is, the exponent of  that produces 1 cannot be 0, since we’ve shown that
that produces 1 cannot be 0, since we’ve shown that  . Therefore, we have a contradiction, and so Euler’s identity must be false, if we assume
. Therefore, we have a contradiction, and so Euler’s identity must be false, if we assume 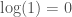 .
.
A New Foundation of Mathematics
I proved the result above about a week ago, but I let it sit on the back burner, because I don’t want to throw Euler, and possibly all complex numbers, under the bus, unless I have a solution. Now I have a solution, and it’s connected to a new theory of mathematics rooted in information theory and what I call “natural units”.
Specifically, given a set of  binary switches, the number of possible states is given by
binary switches, the number of possible states is given by  . That is, if we count all possible combinations of the set of switches, we find it is given by 2 raised to the power of the cardinality of the set. This creates a connection between the units of information, and cardinality. Let’s assume base 2 logarithms going forward. Specifically, if
. That is, if we count all possible combinations of the set of switches, we find it is given by 2 raised to the power of the cardinality of the set. This creates a connection between the units of information, and cardinality. Let’s assume base 2 logarithms going forward. Specifically, if  is a set, we assume the cardinality of
is a set, we assume the cardinality of  , written
, written 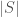 , has units of cardinality or number, and
, has units of cardinality or number, and  has units of bits. Though otherwise not relevant at the moment (i.e., there could be deeper connections), Shannon’s equation for Entropy also implies that the logarithm of a probability has units of bits. Numbers are generally treated as dimensionless, and so are probabilities, again implying that the logarithm always yields bits as its output.
has units of bits. Though otherwise not relevant at the moment (i.e., there could be deeper connections), Shannon’s equation for Entropy also implies that the logarithm of a probability has units of bits. Numbers are generally treated as dimensionless, and so are probabilities, again implying that the logarithm always yields bits as its output.
The question becomes then, what value should we assign to  ? Physically, a system with one state cannot be used to meaningfully store information, since it cannot change states, and as such, the assumption that
? Physically, a system with one state cannot be used to meaningfully store information, since it cannot change states, and as such, the assumption that 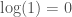 has intuitive appeal. I’m not aware of any contradictions that follow from assuming that
has intuitive appeal. I’m not aware of any contradictions that follow from assuming that 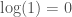 (other than Euler’s identity), so I don’t think there’s anything wrong with it, though this of course doesn’t rule out some deeply hidden contradiction that follows.
(other than Euler’s identity), so I don’t think there’s anything wrong with it, though this of course doesn’t rule out some deeply hidden contradiction that follows.
However, I’ve discovered that assuming  implies true results. Physically, the assertion that
implies true results. Physically, the assertion that  is stating that, despite not having the ability to store information, a system with one state still carries some non-zero quantity of information, in the sense that it exists. As we’ll see,
is stating that, despite not having the ability to store information, a system with one state still carries some non-zero quantity of information, in the sense that it exists. As we’ll see,  cannot be a real number, and has really unusual properties that nonetheless imply correct conclusions of mathematics.
cannot be a real number, and has really unusual properties that nonetheless imply correct conclusions of mathematics.
If we assume that  , it must be the case that
, it must be the case that  . We can make sense of this by assuming that
. We can make sense of this by assuming that 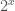 is defined over
is defined over  , other than at
, other than at  , where it is simply undefined. This makes physically intuitive sense, since you cannot apply an operator a zero number of times, and expect a non-zero answer, at least physically. To do something zero times is to do literally nothing, and so the result must be whatever you started with, which is not exactly zero, but it cannot produce change. Now you could argue I’ve just made up a new number, but so what? That’s precisely the point, because it’s more physically intuitive than standard axioms, and as we’ll show, it implies true results. Further, interestingly, it implies the possibility that all of these numbers are physically real (i.e., negative and complex numbers), though they don’t have any clear expression in Euclidean 3-space (e.g., even credits and debits are arguably better represented as positive magnitudes that have two directions). That is, the assumption is that things that exist always carry information, which is not absurd, physically, and somehow, it implies true results of mathematics.
, where it is simply undefined. This makes physically intuitive sense, since you cannot apply an operator a zero number of times, and expect a non-zero answer, at least physically. To do something zero times is to do literally nothing, and so the result must be whatever you started with, which is not exactly zero, but it cannot produce change. Now you could argue I’ve just made up a new number, but so what? That’s precisely the point, because it’s more physically intuitive than standard axioms, and as we’ll show, it implies true results. Further, interestingly, it implies the possibility that all of these numbers are physically real (i.e., negative and complex numbers), though they don’t have any clear expression in Euclidean 3-space (e.g., even credits and debits are arguably better represented as positive magnitudes that have two directions). That is, the assumption is that things that exist always carry information, which is not absurd, physically, and somehow, it implies true results of mathematics.
Again,  , and so
, and so  , which implies that
, which implies that  , and as such,
, and as such,  . If we consider
. If we consider  , we will find two correct results, depending how we evaluate the expression. If we evaluate what’s under the radical first, we have
, we will find two correct results, depending how we evaluate the expression. If we evaluate what’s under the radical first, we have  . If however we evaluate
. If however we evaluate  , we instead have
, we instead have  , which is also correct. I am not aware of any number that behaves this way, producing two path-dependent but correct arithmetic results. Finally, because
, which is also correct. I am not aware of any number that behaves this way, producing two path-dependent but correct arithmetic results. Finally, because  , it follows that
, it follows that  , and so
, and so  , where
, where  .
.
As a general matter, given  , we have
, we have  . Exponentiating, we find
. Exponentiating, we find  , but it suggests that
, but it suggests that  is an iterator, that gives numbers physical units, in that
is an iterator, that gives numbers physical units, in that  is not dimensionless, though it is unitary.
is not dimensionless, though it is unitary.
This is clearly not a real number, and I’m frankly not sure what it is, but it implies true results, though I am in no position to prove that it implies a consistent theory of arithmetic, so this is just the beginning of what I hope will be a complete and consistent theory of mathematics, in so far as is possible, fully aware that the set of theorems on integers is uncountable, whereas the set of proofs is countable.
Information, Fractional Cardinals, Negative Cardinals, and Complex Cardinals
In a paper titled Information, Knowledge, and Uncertainty, I presented a tautology that connects Information  , Knowledge
, Knowledge  , and Uncertainty
, and Uncertainty  , as follows:
, as follows:
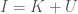 .
.
The fundamental idea is that a system will have some quantity of information 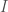 that can be known about the system, and so everything I know about the system
that can be known about the system, and so everything I know about the system  plus what I don’t know about the system
plus what I don’t know about the system  must equal what can be known about the system. Specifically, we assume that
must equal what can be known about the system. Specifically, we assume that  , where
, where  is the set of states of the system in question. This turns out to be empirically true, and you can read the paper to learn more. Specifically, I present two methods for rigorously calculating the values
is the set of states of the system in question. This turns out to be empirically true, and you can read the paper to learn more. Specifically, I present two methods for rigorously calculating the values  and
and 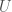 , one is combinatorial, and the other is to use Shannon’s entropy equation for
, one is combinatorial, and the other is to use Shannon’s entropy equation for 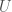 . The results clearly demonstrate the equation works in practice, in addition to being philosophically unavoidable.
. The results clearly demonstrate the equation works in practice, in addition to being philosophically unavoidable.
Because 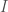 will have units of bits,
will have units of bits,  and
and 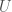 must also have units of bits. Therefore, we can exponentiate the equation using sets
must also have units of bits. Therefore, we can exponentiate the equation using sets  and
and  , producing the following:
, producing the following:
 , where
, where  ,
,  , and
, and  .
.
Even if we restrict 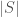 to integer cardinalities, which makes perfect sense because it is the number of states the system in question can occupy, it is possible for either of
to integer cardinalities, which makes perfect sense because it is the number of states the system in question can occupy, it is possible for either of  and
and  to have a rational number cardinality. The argument is, exponentiating by some number of bits produces cardinalities. Because both
to have a rational number cardinality. The argument is, exponentiating by some number of bits produces cardinalities. Because both  and
and 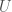 have units of bits, regardless of their values, if we assume the relationship between information and number holds generally, it must be the case that there are cardinalities
have units of bits, regardless of their values, if we assume the relationship between information and number holds generally, it must be the case that there are cardinalities  and
and  . Because either could be a rational number, we must accept that rational cardinalities exist, given that the equation
. Because either could be a rational number, we must accept that rational cardinalities exist, given that the equation 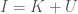 is true, both empirically and philosophically. The same is true of negative cardinalities and complex cardinalities given the arguments above regarding
is true, both empirically and philosophically. The same is true of negative cardinalities and complex cardinalities given the arguments above regarding  , though there seems to be an important distinction, which is discussed below.
, though there seems to be an important distinction, which is discussed below.
Inconsistency between Assumptions Regarding the Logarithm
It just dawned on me, after writing the article, that the discussion above presents what seem to be two independent, and inconsistent axioms regarding the logarithm. Specifically, the exponentiated equation  requires that
requires that  . As an example, let’s assume we’re considering a set of
. As an example, let’s assume we’re considering a set of  boxes, one of which contains a pebble, and we’re interested in the location of the pebble. As described, this system has
boxes, one of which contains a pebble, and we’re interested in the location of the pebble. As described, this system has  possible states (i.e., locations of the pebble) and, therefore
possible states (i.e., locations of the pebble) and, therefore  .
.
Now assume you’re told (with certainty) that the pebble is not in the first box. You are now considering a system with 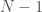 possible states, and so your uncertainty has been reduced. However, because this information doesn’t change the underlying system in any way, and in general,
possible states, and so your uncertainty has been reduced. However, because this information doesn’t change the underlying system in any way, and in general, 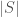 cannot change as a result of our knowledge of the system, it must be the case that your Knowledge is given by
cannot change as a result of our knowledge of the system, it must be the case that your Knowledge is given by  , which is non-zero. We can then reasonably assume that
, which is non-zero. We can then reasonably assume that  contains
contains  states, and that
states, and that  . Now assume you’re told that all but one box has been eliminated as a possible location for the pebble. It follows that
. Now assume you’re told that all but one box has been eliminated as a possible location for the pebble. It follows that  , and that
, and that  . If
. If  is not zero,
is not zero, 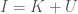 fails. Because it is a tautology, and empirically true, it must be the case that
fails. Because it is a tautology, and empirically true, it must be the case that 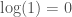 , which is plainly not consistent with the arguments above regarding
, which is plainly not consistent with the arguments above regarding  .
.
Now you could say  is a bunch of garbage, and that’s why we have already found a contradiction, but I think that’s lazy. I think the better answer is that
is a bunch of garbage, and that’s why we have already found a contradiction, but I think that’s lazy. I think the better answer is that 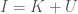 governs representations, not physical systems, and is only true with regards to representations of physical systems. We can then conclude that
governs representations, not physical systems, and is only true with regards to representations of physical systems. We can then conclude that 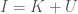 applies only to representations of physical systems, as an idea. Because
applies only to representations of physical systems, as an idea. Because  is rooted in a physically plausible theory of the logarithm, we can say that this other notion of the logarithm governs physical systems, but does not govern representations of physical systems, since it clearly leads to a contradiction.
is rooted in a physically plausible theory of the logarithm, we can say that this other notion of the logarithm governs physical systems, but does not govern representations of physical systems, since it clearly leads to a contradiction.
The question is then, as a matter of pure mathematics, are these two systems independent? If so, then we have something like the Paris Harrington Theorem. At the risk of oversimplification, the idea is that the mathematics that governs our reality in Euclidean 3-space could be different than the Platonic mathematics that governs representations, or perhaps ideas generally.
I’ll note that 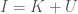 is a subjective measure of information related to a representation of a system, in that while
is a subjective measure of information related to a representation of a system, in that while 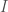 is an objective invariant of a system,
is an objective invariant of a system,  and
and 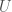 are amounts of information held by a single observer. In contrast,
are amounts of information held by a single observer. In contrast,  is rooted in the physically plausible argument that if a thing exists in Euclidean 3-space (i.e., it has some measurable quantity), then it must carry information, even if it is otherwise static in all other regards.
is rooted in the physically plausible argument that if a thing exists in Euclidean 3-space (i.e., it has some measurable quantity), then it must carry information, even if it is otherwise static in all other regards.
Interestingly, if we accept the path-dependent evaluation of  , and we believe that
, and we believe that  is the result of a physically meaningful definition of the logarithm, then this could provide a mathematical basis for non-determinism, in that physical systems governed by
is the result of a physically meaningful definition of the logarithm, then this could provide a mathematical basis for non-determinism, in that physical systems governed by  (which is presumably everything, if we accept that all extant objects carry information), allow for more than one solution, mechanically, in at least some cases. And even if it’s not true non-determinism, if we view 1 in the sense of being the minimum amount of energy possible, then
(which is presumably everything, if we accept that all extant objects carry information), allow for more than one solution, mechanically, in at least some cases. And even if it’s not true non-determinism, if we view 1 in the sense of being the minimum amount of energy possible, then  is definitely a very small amount of information, which would create the appearance of non-determinism from our scale of observation, in that the order of interactions would change the outcomes drastically, from -1 to 1.
is definitely a very small amount of information, which would create the appearance of non-determinism from our scale of observation, in that the order of interactions would change the outcomes drastically, from -1 to 1.
In closing, I’ll add that in the exponentiated form,  , neither set can ever be empty, otherwise we have an empty set
, neither set can ever be empty, otherwise we have an empty set  , which makes no sense, because again, the set can’t change given our knowledge about the set. Once we have eliminated all impossible states,
, which makes no sense, because again, the set can’t change given our knowledge about the set. Once we have eliminated all impossible states,  will contain exactly one element, and
will contain exactly one element, and  will contain all other elements, which is fine. The problem is therefore when we begin with no knowledge, in which case
will contain all other elements, which is fine. The problem is therefore when we begin with no knowledge, in which case  , in the sense that all states are possible, and so our uncertainty is maximized, and our knowledge should be zero. However, if
, in the sense that all states are possible, and so our uncertainty is maximized, and our knowledge should be zero. However, if  is empty, then we have no definition of
is empty, then we have no definition of  .
.
We instead assume that  begins non-empty, ex ante, in that it contains the cardinality of
begins non-empty, ex ante, in that it contains the cardinality of  , which must be known to us. Once our knowledge is complete,
, which must be known to us. Once our knowledge is complete,  will contain all impossible states of
will contain all impossible states of  , which will be exactly
, which will be exactly  in number, in addition to the cardinality of
in number, in addition to the cardinality of  , which was known ex ante, leaving one state in
, which was known ex ante, leaving one state in  , preserving the tautology of both
, preserving the tautology of both 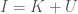 and
and  .
.
and
, respectively. Let’s further assume that we are surrounded almost exclusively by positive mass, which again is denoted by
. Let’s assume that positive mass is attracted to positive mass, which would obviously be perfectly consistent with gravity, since we’ve already assumed that almost all matter we are exposed to is positive mass. Further, let’s assume that negative mass is similarly attracted to negative mass, and that masses with opposite signs cause repulsion. That is, given some quantity of positive mass
and negative mass
, the two masses will repel each other when sufficiently proximate. This completes the symmetry of gravity, since we now have positive and negative masses, and attractive and repulsive forces.
to represent a photon, we could write that
, to represent a positron and electron colliding to form a photon. Similarly, we could write that
to represent a light on light collision producing an electron-positron pair.
and
. The question is, what do we get when we combine the negative-mass versions of an electron and positron? Expressed symbolically,
, where
is some unknown particle.
, as a particle distinct from ordinary light. Specifically, if we further posit that negative-mass light does not interact with positive mass, and that positive-mass light (our ordinary photons) do not interact with negative mass, then that negative mass would not be detectable using ordinary photons. Ironically, this is a kind of “dark” matter, but it’s not the nonsense hypothesized hitherto.