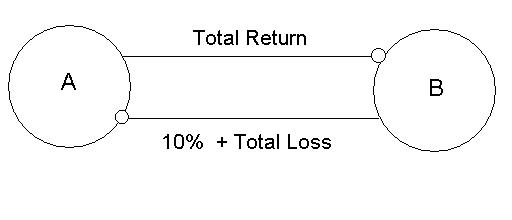Email: derivativedribble [at] yahoo [dot] com.
Twitter: My Profile
Friday June 26, 2009
Friday May 29, 2009
My latest for the Atlantic: Could Government Intervention Help Markets Function Better?
Saturday May 16, 2009
My latest for the Atlantic: How NPR Mangled Geithner’s Plan For OTC Derivatives
Thursday May 7, 2009
My latest for the Atlantic: Boring Banking Will Not Save You
Friday May 1, 2009
My latest for the Atlantic: The Sorry State Of The Dismal Science
Thursday April 30, 2009
Friday April 17, 2009
My Latest for the Atlantic: Credit Default Swaps and Control Rights
Tuesday April 14, 2009
My latest for the Atlantic: The Art of the Banking Controversy
Friday April 10, 2009
My latest for the Atlantic: The Regulatory Pendulum and Electoral Guillotine
Wednesday April 8, 2009
Friday April 3, 2009
Very nice chart from the FT on debt and demographics
Monday March 30, 2009
Recommended: FT interview with Obama
Friday March 27, 2009
My latest for the Atlantic Business
Wednesday March 25, 2009
High speed photos of exploding objects
Bank Executive’s home vandalized
MUST READ: Resignation letter of form AIGFP employee
HIGHLY RECOMMENDED: John Authers takes a look at the EMH and the future of wealth management
Friday March 20, 2009
HIGHLY RECOMMENDED: Washington Post takes us inside AIG-FP (“If they give back the money, then they will walk. And they will walk into the arms of AIG’s counterparties.”)
My latest for The Atlantic
HIGHLY RECOMMENDED: This Blog
Tuesday March 17, 2009
Fortune does a good job getting the facts straight about CDS
Friday March 13, 2009
Recommended: The Economist takes a look at credit markets
Thursday March 12, 2009
Gates back on top as crisis wipes out other billionaires
Monday March 9, 2009
Friday March 6, 2009
Alpha Ville on the ocean of looming corporate defaults
Thursday March 5. 2009
Wednesday March 4, 2009
Tuesday March 3, 2009
Derivatives market remains profitable business for J.P. Morgan
Very interesting data on the multiplier effect from the CBO
Tuesday February 24, 2009
My latest article for the Atlantic
Monday February 23, 2009
HIGHLY RECOMMENDED: Howard Davies, head of LSE and former FSA Chairman, on bank regulation
FT on the prospect of a depression in Spain
Rick Santelli rouses traders over Obama’s housing plan
Sunday February 22, 2009
Citi in talks with U.S. Government over common equity stake
Thursday February 19, 2009
Must read: Buiter rips apart Obama’s housing plan
Saturday February 14, 2009
Collective decision making in animals and humans
Thursday February 12, 2009
New York edges closer to expanding rent control
Wednesday February 11, 2009
Rep. Kanjorski tells us how close to the edge we were
Treasury’s 6 and a half page plan to save the world
Tuesday February 10, 2009
Great article by the FT’s John Authers on the prospects of an equity bounce-back
Friday February 5, 2009
Wednesday February 4, 2009
My latest article for the Atlantic Business Channel
Tuesday February 3, 2009
Monday February 2, 2009
For my fellow music lovers: Classic Arts Showcase on YouTube
S&P says 200 defaults expected
Thursday January 30, 2009
Crash like this expected only once over next 34,000 years
Contraction bad, but better than expected
Wednesday January 28, 2009
John Authors on the perception of a bargain
Capacity drops in France and Italy
World growth worst in 60 years
Tuesday January 27, 2009
Madoff Jr. gets busted in $400 million Ponzi scheme
Great article from Atlantic’s new business section
Monday January 26, 2009
Iceland’s government tumbles under pressure
Unemployment rate looms over banking sector
Wednesday January 23, 2009
Obama thinks stimulus package could be ready mid February
Muni derivatives under investigation
Very interesting John Authers video on the prospect of a slow down in China
U.K. officially in a recession
Wednesday January 22, 2009
N.Y. Times provides some perspective on the severity of the crisis
U.S. accuses China of currency manipulation
Tuesday January 21, 2009
Bank market capitalization, then and now
John Authers article and video on the second wave of banking turmoil
Monday January 20, 2009
Thursday January 15, 2009
California to go insolvent in weeks
Big numbers for foreclosures in 2008
The wealthy slammed by the down turn
Wednesday January 14, 2009
Credit markets show signs of life despite rest of world
Martin Wolf takes on Obama’s stimulus package
CDS market predicts bleak future for sovereigns
Tuesday January 13, 2009
Still no Russian gas flowing into E.U.
Pension funds hammered, seek Federal money
Release of TARP funds faces stiff opposition
Bernanke says fiscal measures not enough
Monday January 12, 2009
John Authers takes a look at sovereign default and the Euro
Proprietary trading winding down
Banks suspected in facilitating purchase of weapons for Iran
Barney Frank proposes drastic changes to TARP and Hope For Homeowners Act (a summary of the bill and the actual text can be found here)
Friday January 9, 2009
Cash flowing back to emerging markets
Obama puts pressure on Congress over stimulus package
Congress points fingers at Treasury over TARP
Thursday January 8, 2009
Citi supports bankruptcy law reform
Very interesting article on government bonds
Wednesday January 7, 2009
BofA finally sells stake in Chinese Bank
A closer look at Larry Summers
German bond auction fails: bad sign for sovereigns
Tuesday January 6, 2009
Pending home sales drop to record lows
Monday January 5, 2009
A bit of unexpected historical perspective on the credit crisis
Wednesday December 31, 2008
John Authers constructs a timeline of the disasters of 2008
Steepest drop ever for commodities
Muni market dries up as states face looming budget gaps
Paulson says U.S. lacked tools to handle crisis
Tuesday December 30, 2008
Good series of video interviews of Roubini
Automakers consider change to supply model to prevent supply-side failures
The economics of climate change
Monday December 29, 2008
Retail bankruptcies and store closings on the rise
Corporate profits likely to continue losing streak
Conventional media outlets seek partnership with internet big wigs
John Authers sees gloomy future for equities
Tuesday December 23, 2008
U. Chicago points fingers at the bailout
Interactive applet rating financial big wigs
Monday December 22, 2008
Pound sinks to record low against basket of currencies
Toyota predicts first loss ever
Oil continues to slide despite OPEC cuts
Friday December 19, 2008
Early Christmas for automakers
Thursday December 18, 2008
Gather ye rosebuds while ye may
Mining sector calls for unprecedented cut backs
Wednesday December 17, 2008
Tis dangerous on the high seas!
Tuesday December 16, 2008
Monday December 15, 2008
Derivative Dribble spots economic news faster than the MSM
Friday December 12, 2008
Bifurcation of the debt markets
Goldman predicts slow recovery for oil
The ever entertaining Jim Rogers
India gets roped into the slow down
Senate puts the brakes on the Big 3
Thursday December 11, 2008
This time the floor is falling
Wednesday December 10, 2008
The beginning of a market for toxic instruments?
Deflationary pressure in China?
Tuesday December 9, 2008
Russia walks the sovereign plank: debt downgraded
OTC commodities central clearing house ready for launch
Corporate default rates set to rise
Monday December 8, 2008
BREAKING NEWS: Federal legislation proposed to regulate OTC Market
The invisible hand and the sovereign strangle
Video game nerds prove recession proof
Friday December 5, 2008
More truly awful news, this time it’s California
Distraction from all the bad news
Thursday December 4, 2008
Black Friday yields red November for retail
China Investment Corp won’t invest in U.S. financial institutions
Wednesday December 3, 2008
Great explanation of Money Markets
Real yield on Treasuries dip into negative territory
Tuesday December 2, 2008
The ever increasing interest in CDS
Monday December 1, 2008
BRIC nations to offer consumption through downturn
The Swiss financial throne under siege
Wednesday November 26, 2008
Shift from OTC to exchanges gains more momentum
Tuesday November 25, 2008
New lending facility for instruments backed by consumer debt
Monday Novemer 24, 2008
Buffett discloses info on Berkshire’s portfolio of financial weapons of mass destruction
More historical data on declines
Citi gets early Christmas present and Paulson works another weekend
Friday November 21, 2008
Goldman predicts bleak outlook for U.S. Economy
Thursday November 20, 2008
Slightly cooler heads in Iceland after IMF/Nordic bailout
The CDS Market becomes the new economic indicator
I’ve seen more and more of this type of analysis. The CDS market is becoming more and more relevant as an economic indicator. Keep up the good work Alpha Ville!
Inventories Swell Kudos to Naked Capitalism!
Wednesday November 19, 2008
CDS markets predict bleak future
CDS clearing house seems likely
Tuesday November 18, 2008
Detroit gets coals for Christmas
Japan wins economic beauty contest
Historical perspective on volatility
Monday November 17, 2008
Highly recommended: Interviews with Jim Rogers
The dangers of subjective valuation
Good article, even though I disagree
New York City real estate falls from grace
Friday November 14, 2008
Eurozone in technical recession
Thursday November 13, 2008
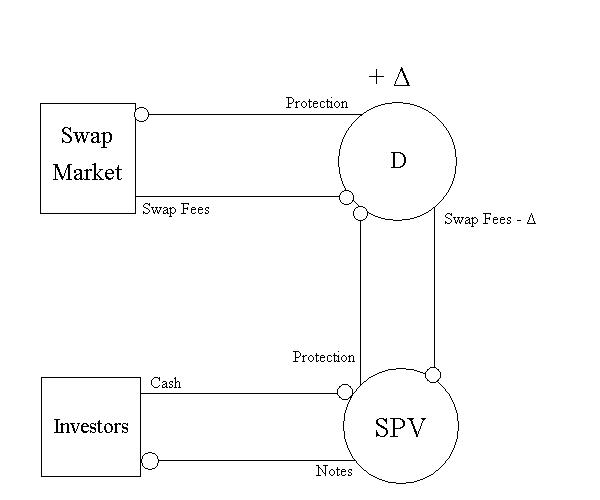
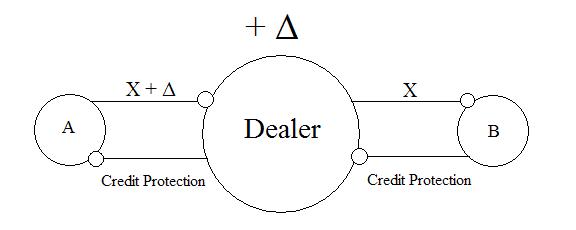
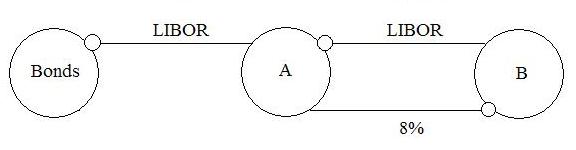
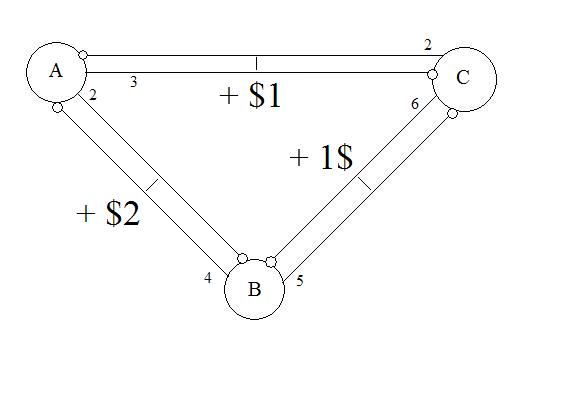
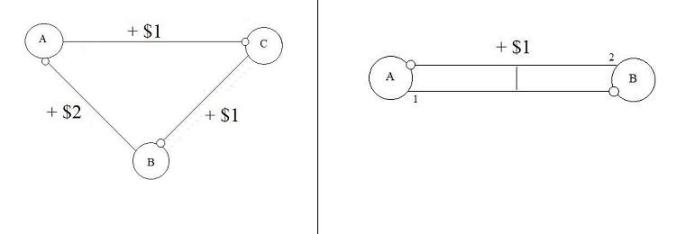
More complex than a synthetic CDO
Derivative Dribble considers asking Fed for money
Germany in technical recession
Greenwich points to Wall Street
Would be CDS regulator vindicated (?)