In a previous note, I pointed out that many (and possibly nearly all) human mtDNA genomes “begin” (i.e., despite its circularity) with exactly the same 15 bases:

GATCACAGGTCTATC

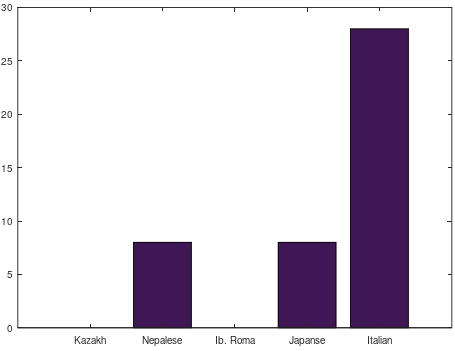
In fact, because it’s circular, it makes perfect sense that there is a starting index, otherwise you run the risk of beginning protein production at different indexes, given the same genome, thereby producing different proteins. Other species seem to have their own opening ledes as well. A very small number of genomes in the NIH database do not contain this lede, but this is extremely rare in what I’m assuming is an enormous database, and though I haven’t done any formal analysis, I’ve found only about a dozen entries that do not contain exactly this sequence in the opening of their ideal alignment, using BLAST. That is, about a dozen genomes still contain this sequence, but not in the opening of the alignment that maximizes the number of matching bases. Further, some Japanese genomes contain minor deletions from this opening sequence, and therefore require minor adjustments to this alignment. In contrast, some of the genomes I found using BLAST require significant adjustments, effectively deleting around 570 bases from the genome, suggesting a significant deviation from a typical human mtDNA genome.

This suggests that as a general matter the correct empirical alignment for the human mtDNA genome begins with this sequence, despite the fact that it is circular, suggesting a useful and arguably “correct” starting point index, and this is in fact reflected in the NIH database, with basically all human mtDNA genomes I’ve found aligned with this opening sequence (including the roughly 200 complete genomes assembled in the dataset below).

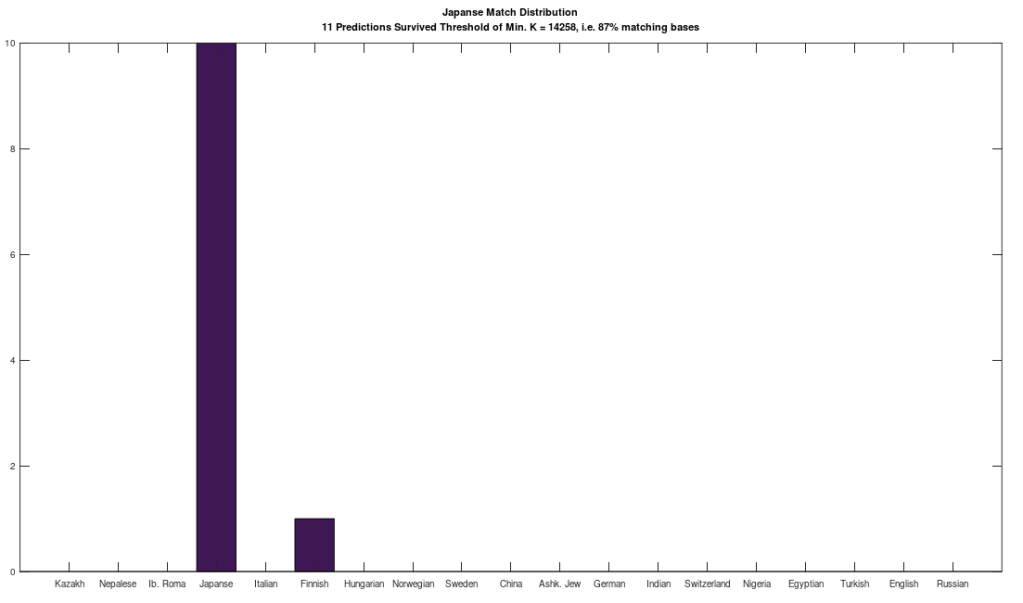
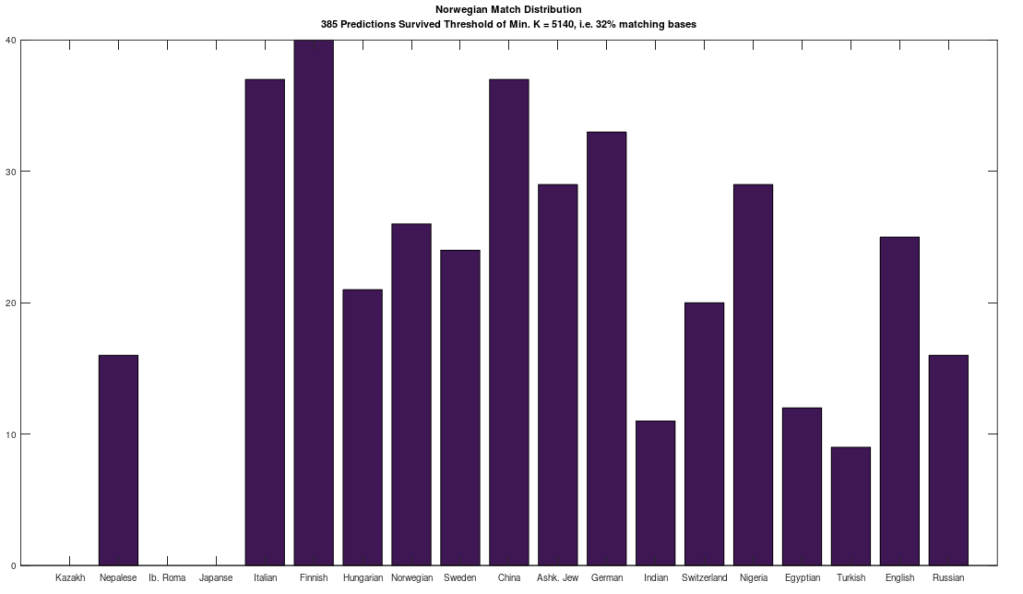
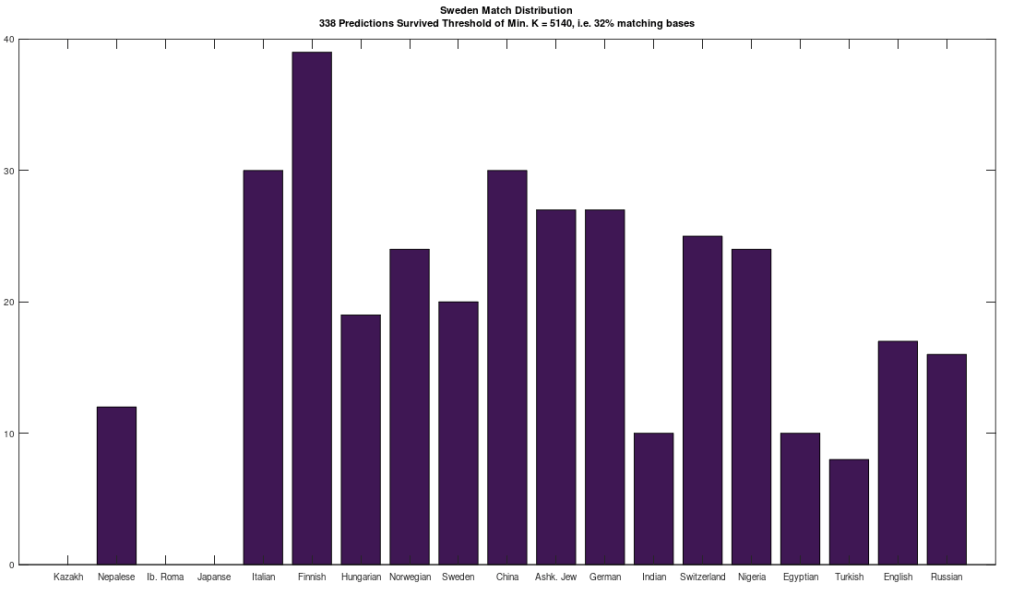
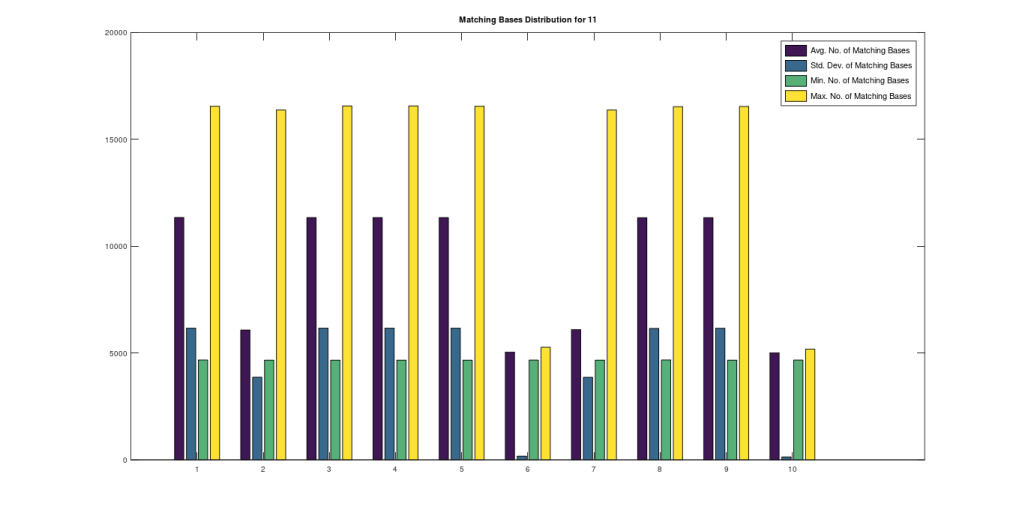
In that same note, I pointed out that if you use this alignment, which the NIH plainly does as a general matter, you find that matching genomes converge to a match, and genomes that don’t match, diverge. Specifically, if you count the average number of bases from index 1 to index K, and increase K, you find that two genomes that in fact have a high number of matching bases produce a curve that plainly converges to around 99% to 100%. In contrast, two genomes that don’t match instead diverge from a high matching percentage to around 25% (i.e., chance). This produces curves that are useful for Machine Learning, since it implies an unsupervised clustering algorithm, where two genomes are clustered together if they produce an upward sloping curve, and otherwise, not clustered together. The plot above shows 10 Nigerian mtDNA genomes compared to a single Japanese genome. The x-axis is the genome index, and the y-axis is the percentage of matching bases, from index 1 up to the x-value. Most of the Nigerian genomes plainly do not match, and so they diverge, whereas some plainly do (converging at the top). There’s also an outlier in the middle, which you can consider as a third class that is a partial match, or simply disregard, as the bottom line is, this produces a useful clustering algorithm.

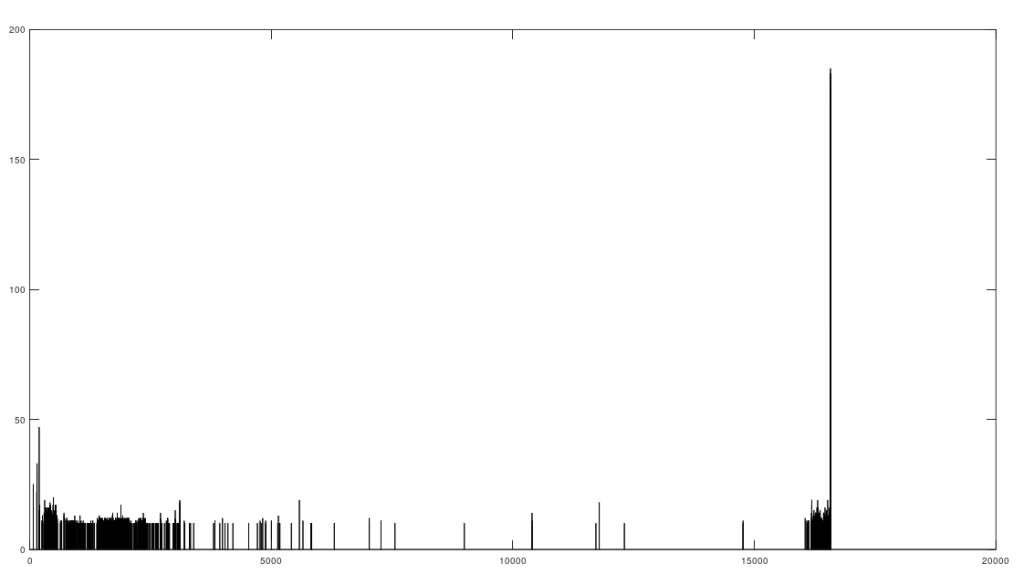
As I tested this more, I realized that you can also build a distribution of the indexes of unequal bases. Specifically, for each genome, run Nearest Neighbor, and find the indexes where that genome and its Nearest Neighbor differ. This will create a distribution, where each index is associated with some number of genome pairs that disagree at that index. The higher that number, the greater the number of instances of unequal bases at that index. When you plot this, you find exactly the same distribution, where the number of anomalously high unequal bases tapers off, which is consistent with the curves plotted above, that produce convergence as a function of index. The bar chart above shows all peaks that exceed the average plus one standard deviation, though you can of course make use of variations on this. Note the peak at the end is due to the fact that basically all of the genomes are missing that entry, causing all of them to be treated as unequal at that index (i.e., the algorithm first calculates equal bases, and disregards all missing entries, causing the compliment to include all instances of missing entries). Considering this further, it implies regions that are common to genomes are found in between the peaks of the chart above. This should make it easy to find genes, and more generally, sequences common to populations, which presumably have some function, even if it’s simply indicative of genetic grouping.

Specifically, the code attached produces 984 roughly homogenous regions. We can then calculate the length of each such region. The total sequence length of the homogenous regions is 15,592 bases, and the total length of the genome is 16,576 bases. This leaves 984 bases unaccounted for, as highly variable regions. This is approximately the length of the D-Loop, also known as the non-coding region, which apparently is a “hot spot for mtDNA alterations“. As a general matter, mtDNA is dense with genes, suggesting that we shouldn’t have too many inconsistent regions, and in fact we don’t. Moreover, you can plainly see that the inconsistent regions become more sparse, with a highly inconsistent and contiguous region in the beginning that could very well be the D-loop.

This is therefore an unsupervised algorithm that apparently correctly partitions this genome.

Here’s the code and the dataset:

https://www.dropbox.com/s/0y881tw2s7w91c8/Temp_CMDNLINE_12_18.m?dl=0

https://www.dropbox.com/s/4m6fhz77ki2rtg8/Genetic_Nearest_Neighbor_Fast.m?dl=0

https://www.dropbox.com/s/4m6fhz77ki2rtg8/Genetic_Nearest_Neighbor_Fast.m?dl=0

https://www.dropbox.com/s/casfm3i07v0vefl/Count_Matching_Bases.m?dl=0

Dataset:

https://www.dropbox.com/s/ht5g2rqg090himo/mtDNA.zip?dl=0

There’s a plain structure to mtDNA, and astonishingly, every genome I’ve seen so far has exactly the same opening sequence of 15 characters, though some Asian peoples have deletions, but they’re otherwise exactly the same –

Literally the exact same opening sequence, globally, and it is as follows:

GATCACAGGTCTATC

This got me thinking that there’s an order to human mtDNA, that variation starts to take place after this opening, as a function of index. It seems that this is in fact the case. Even more interesting, when two genomes match beyond mere change, they produce a convergence towards the overall percentage of matching bases. That is, if you start at index 1, and read to the end of the genome, if two genomes match beyond chance, then the percentage of matching bases from 1 to the end starts to increase at a certain point. If instead, the two genomes have a match that is close to chance (i.e., roughly 1/4 of the bases match), then the percentage of matching bases decreases as a function of index. Here’s a plot of 10 Nigerian mtDNA genomes compared to a single Japanese genome. The x-axis is the genome index, and the y-axis is the percentage of matching bases, from index 1 up to the x-value.

This implies a clustering algorithm, where if the slope is negative on average, then it’s not a match. If instead the slope is positive on average, then there is a match.

Most of the Nigerian genomes are plainly not matches. However, there are two that are a 98% and 100% match to Japanese genomes, respectively (at the top). This implies unquestionable common maternal lineage. There’s a third, that you can see that seems to lag, and then catch up, which has a match percentage of 77%. This obviously implies a bit of judgment, but the algorithm makes perfect sense, and you can deal with these types of issues as you like.

The first and obvious takeaway is that political race is bull shit, and our history is questionable. The scientific takeaway is that mtDNA does seem to follow a chronology, from the first index to the last, and if this is true, then it seems there was an explosion of diversity in maternal lines early in our history, later leading to a convergence, more or less on par with modern maternal lines.

Here’s the code, anything missing (include datasets) can be found in the post just below this one:

https://www.dropbox.com/s/blzcyi7eyuqxu3a/Code%20%281%29.zip?dl=0

The Maritime Archaic mtDNA genomes available from the NIH Database are a 99% match (i.e., 99% of the bases match) for several European, African, and Asian people. Note these are complete genomes, and so it is impossible to deny common ancestry.

This is astonishing, because the strongest match is the Spanish, and this provides irrefutable evidence that people of European descent reached the Americas thousands of years before Columbus, as the Maritime Archaic people are dated somewhere between 7,500 and 3,500 years before present. You’ll also note that the Maritime Archaic samples are a 95% match to Homo Heidelbergensis, which is consistent with the hypothesis that Heidelbergensis is an ancestor common to all of humanity. Each chart shows the number of people in a given population that had a 99% match with the population in question. So the first chart shows the number of people from each population that had a 99% match to at least one Maritime Archaic genome. There are 10 rows in each population, over 17 populations, except for Heidelbergensis, for which only one complete genome is available.

The raw data together with the code and files providing provenance (i.e., direct links to the NIH Database for each row) are all available in two separate zip files:

https://www.dropbox.com/s/e0zf5eokcfdmi7s/MATLAB%20CODE.zip?dl=0

https://www.dropbox.com/s/lxq8gfb4h0p8edw/mtDNA.zip?dl=0

I suppose mtDNA doesn’t control much for superficial appearance, given these results, and the others I’ve been sharing lately, certainly not the factors we typically associate with race, but more remarkably, because it doesn’t change much over generations, it forces us to recognize the brevity of our considerations, that they’re informed by a few centuries or millennia, when the real history of humanity spans hundreds of thousands of years, possibly longer.

Using a simple measure of information, specifically , where is the size of a distribution, and is the entropy of the distribution, the Danes are the most diverse people in the world, with a 99% match to a simply astonishing variety of nationalities. Even more astonishing, if you lower the match threshold to about 95%, you’ll see that many modern populations are a match for Homo Heidelbergensis, an archaic human that was thought to have gone extinct hundreds of thousands of years ago, though it’s quite clear many modern humans are basically indistinguishable on their maternal line from this otherwise archaic species.

I suppose mtDNA doesn’t control much in the way of superficial appearance, given these results, and the others I’ve been sharing lately, certainly not the factors we typically associate with race, but more remarkably, because it doesn’t change much over generations, it forces us to recognize the brevity of our considerations, that they’re informed by a few centuries or millennia, when the real history of humanity spans hundreds of thousands of years, possibly longer. It’s not that this line of study doesn’t divide humanity, as it certainly does, but not along any political or racial basis I’ve seen before. Instead, more than anything else, it shows that our ideas of race are totally unscientific, and basically a myth.

I’ve updated the dataset to include the raw genomes and the provenance for each file, with a link to the NIH database entry for each row.

Enjoy!

https://www.dropbox.com/s/ht5g2rqg090himo/mtDNA.zip?dl=0

It turns out the Japanese do have unique mtDNA, but the alignment data provided by the NIH hides this, because it presents the first base of the genome as the first index, without any qualification, as there’s an obvious deletion to the opening sequence of bases. Maybe this is standard, but it’s certainly confusing, and completely wrecks small datasets, where you might not have another sequence with the same deletion. The NIH of course does, and that’s why BLAST returns perfect matches for genomes that contain deletions, and my software didn’t, because I only have 185 genomes.

The underlying paper that the genomes are related to is here:

https://pubmed.ncbi.nlm.nih.gov/34121089/

Again, there’s a blatant deletion in many Japanese mtDNA genomes, right in the opening sequence. This opening sequence is perfectly common to all other populations I sampled, meaning that the Japanese really do have a unique mtDNA genome.

Here’s the opening sequence that’s common globally, right in the opening 15 bases:

GATCACAGGTCTATC

For reference, here’s a Japanese genome with an obvious deletion in the first 15 bases, together for reference with an English genome:

https://www.ncbi.nlm.nih.gov/nuccore/LC597333.1?report=fasta

https://www.ncbi.nlm.nih.gov/nuccore/MK049278.1?report=fasta

Once you account for this by simply shifting the genome, you get perfectly reasonable match counts, around the total size of the mtDNA genome, just like every other population. That said, it’s unique to the Japanese, as far as I know, and that’s quite interesting, especially because they have great health outcomes as far as I’m aware, suggesting that the deletion doesn’t matter, despite being common to literally everyone else (as far as I can tell). Again, literally every other population (using 185 complete genomes) has a perfectly identical opening sequence that is 15 bases long, that is far too long to be the product of chance.

Here’s the updated software that finds the correct alignment accounting for the deletion:

https://www.dropbox.com/s/2lwgtjbzdariiik/Japanese_Delim_CMDNLINE.m?dl=0

I noticed that some Japanese people seem to have a very low number of bases in common with not only the world, but each other. The dataset I’m using consists of 185 complete genomes, from 19 nationalities, and 3 ancient species, all taken from the NIH Database.

For 2 of the 10 Japanese complete genomes, the maximum number of matching bases anywhere in the world is about 5,000 matching bases. The complete genome has a size of 16,579 bases, and so this is not much better than chance, given by 16,579/4 = 4.145, suggesting that it really is just the operation of chance causing any intersection at all between those Japanese genomes and the global population generally.

This view finds further support in the fact that the entire global population has a perfectly consistent genome (i.e., no variation at all) over the first 15 bases. The probability of this being chance is 1/4¹⁹⁰, which is so small, it’s zero in MATLAB. That is, the sequence has a length of 15, and it is common to 175 genomes.

Note this dataset includes 3 complete ancient genomes, specifically, Denisovan, Maritime Archaic, and Homo heidelbergensis, all of which also contain exactly the same globally common sequence. Homo heidelbergensis is thought to have gone extinct hundreds of thousands of years ago, suggesting there is basically zero variation in the opening prefix to human mtDNA.

Said otherwise, globally, there is no mutation at all over the first 15 bases of the human mtDNA genome, anywhere in known history.

This is not true when you include Japan, and in fact, only 1 genome out of 10 is a perfect match, and therefore consistent with the global genome. Instead, the average number of matches excluding that one individual, is 3.2, over the opening prefix of 15 bases.

Putting it all together, you have a global match count for 2 out of 10 Japanese people that seems to be the result of pure chance, and 9 out of 10 Japanese people have a prefix segment that is almost entirely inconsistent with a globally and historically uniform segment of mtDNA.

Has anyone noticed this before or heard other people discussing it? I think it’s consistent with one of two hypotheses:

1. Japanese mtDNA has a much higher rate of mutation than typical mtDNA, for whatever reason. We could test for this by looking at the rate of change from one generation to the next.
2. Japanese mtDNA descends from a totally different bacteria.
3. There was an event that caused a drastic mutation to Japanese mtDNA, and then natural selection took over, and so nothing much changed, since as far as I know, the Japanese have no drastically higher rates of diseases connected to mtDNA, and in fact they have good health outcomes overall.

If either 1 or 3 are true, then it suggests that DNA could have an error correcting function, since single base variants often produce disease, yet here we have drastically inconsistent mtDNA, that doesn’t seem to have any notable problems at all. Note that natural selection would certainly kill off bad outcomes, but it doesn’t produce good outcomes. And so this particular case is at least consistent with the idea that DNA can adjust mutated sequences to avoid malfunction and disease.

In any case, this is highly unusual, since mtDNA is consistent for generations, and in some cases over possibly hundreds of thousands of years. I’ll add the caveat that it could be bad data, despite being from a reputable source, and the opening prefix being inconsistent is perhaps evidence of this.

Here’s the dataset with a ton of code you can use to analyze the data, and here’s the search string for the raw data from the NIH Database.

I’m still tweaking this, but this is an algorithm for finding common ancestry given mtDNA (it will not work otherwise), and the best fit for a common ancestor to a population.

https://www.dropbox.com/s/yxvqgt73gfxxqlo/Root_Testing_CMNDLINE.m?dl=0

I’ve never been able to prove formally why my unsupervised classification algorithm works, and in fact, I’ve only been able to provide a loose intuition, rooted in how I discovered it: as you tighten the focus of a camera lens, the changes near the correct focus are non-linear, in that the object quickly comes into focus. And so I searched for the greatest change in the structure of a dataset as a function of discernment, which works incredibly well, especially for an unsupervised algorithm. In contrast, the supervised version of that algorithm has a simple proof, which you can find in my paper Analyzing Dataset Consistency. However, it just dawned on me, I think I explained why it works, though it’s not a formal proof, in my other paper, Information, Knowledge and Uncertainty. Specifically, the opening example I give is a set of boxes, one of which contains a pebble, where the task is to guess which box the pebble is in. If someone tells you that the pebble is not in the i-th box, then your uncertainty is reduced. But the reason it’s reduced is because the system is now equivalent to a system with one less box. In contrast, the rest of the examples I give in that paper, deal with static observations that have some fixed uncertainty.

Applying this to my unsupervised clustering algorithm, the point at which the entropy changes the most (i.e., Uncertainty), is also the point at which your Knowledge changes the most, due to the simple equation . As a consequence, my unsupervised clustering algorithm finds the point at which your knowledge changes the most as a function of the structure of the dataset. All points past that, reduce the size, and therefore information content of the clusters, without materially adding to Knowledge. Specifically, if you unpack the equation a bit more, , where is the number of states of the system. In the case of the box example, is the number of boxes when there’s one pebble. In the case of a distribution, it’s the total number of elements in the distribution. And as you’re increasing the threshold for inclusion in a cluster, the cluster size shrinks, thereby decreasing . If it turns out that the size of the problem space generally decreases faster than the entropy (i.e., Uncertainty U), then your Knowledge actually decreases as the problem space decreases in size. As a consequence, the unsupervised algorithm finds the point where the entropy of the problem space changes the most as a function of the threshold for inclusion, which is the point where you get the most Knowledge per unit of change. I suppose upon reflection, the correct method is to find the point where the entropy of the problem space changes the most as a function of the size of the problem space. That said, my software plainly works, so there’s that.

In any case, this is not a proof, but it is a mathematical explanation. What I’m starting to come around to, is the idea that some phenomena, perhaps even some algorithms, function as a consequence of epistemological truths of reality itself. You can definitely accuse me of laziness, in that I can’t formally prove why the algorithm works, but that dismisses the possibility that some things might be true from first principles that defy any further logical justification, in that they form axioms consistent with reality itself. In that case, there is no proof beyond the empirical fact that Knowledge changes sub-optimally past the point identified by the algorithm. The reason I believe this is possible, is because the equation , follows solely from the tautology that all things are either in a set, or not, and there is, as far as I know, no other proof that this is true. Moreover, the equation works, empirically, so it is in this view an equation that has no further logical justification, that operates like an equation of physics. The more general premise at least suggests the possibility of algorithms that defy further logical justification beyond empiricism.

The reason I thought of this, is because I was working on clustering populations on the basis of mtDNA, and I noticed the same thing happen that happened when I first started my work in A.I. –

There was a massive discontinuous change in cluster entropy, as a function of the inclusion threshold. When I looked at the results, it produced meaningful population clusters, where e.g., both Japanese and Finnish people are treated as homogenous, and basically everyone else is heterogenous. This was totally unsupervised, with no information at all, other than raw mtDNA, and it’s obviously correct. Moreover, Sweden and Norway produced basically the same heritage profile, and even terminate at exactly the same iterator value –

This is consistent with the fact that Norwegians and Swedes are genetically closer to each other than they are to the Finns. The Finns also speak a totally different, Uralic language, whereas Norwegian and Swedish are both Germanic, and so in this case, heritage follows language, which is not necessarily always true, for the simple reason of conquest. For example, the Swedes and Norwegians had their own alphabet, the Runic Scripts, and now they don’t, they use the Latin alphabet like everyone else, because of what is basically conquest.

Above are the plots for the Finnish, Japanese, Swedish, and Norwegian heritage profiles I mentioned, and below is the code and a link to the dataset. You might be wondering how it is that of the few populations that map to Finland, Nigeria is among them. Well, it turns out, 87% of the complete Finnish mtDNA genome maps to a 2,000 year old Ancient Egyptian genome. They also map basically just as closely to modern Egyptians. All of this data is from the National Institute of Health, and you can find all of it by entering the following search query into the NIH Database:

ETHNICITY AND ddbj_embl_genbank[filter] AND txid9606[orgn:noexp] AND complete-genome[title] AND mitochondrion[filter]

Just replace ETHNICITY with Norway, Egypt, etc. Isn’t life something when you actually do the work.

Here’s the code:

https://www.dropbox.com/s/h8ae0tuvtoa1bk1/Percentage_Based_Clustering_CMDNLINE.m?dl=0

Here’s the dataset:

https://www.dropbox.com/s/mj8qk8jxybc9wbc/MTDNA.txt?dl=0

The dataset now includes 19 ethnicities (listed below), and it’s simply fascinating to dig into, and there’s a bunch of software in the previous posts you can use to probe it.

Kazakh, Nepalese, Iberian Roma, Japanese, Italian, Finnish, Hungarian, Norwegian, Sweden, Chinese, Ashkenazi Jewish, German, Indian, Switzerland, Nigerian, Egyptian, Turkish, English, Russian.

I noticed that when you compare a population to itself, at least using mtDNA, it produces a characteristic profile that is unique to the population, as shown in the graph below that plots the results of comparing the mtDNA (full genome) of 10 Swiss people to each other.

Specifically, when counting matching bases between a given row (i.e., individual), and the rest of its population, the average (A), standard deviation (S), minimum (m), and maximum (M) of the number of matching bases, viewed as a vector , forms a unique profile for each population. Intuitively, each genome in a population has a roughly similar relationship to all the other genomes in the population, producing a signature profile pattern of the form in the graph above. However, sometimes you see multiple patterns within a given population, which also works for purposes of ML, since all you need is one pattern that pops up more than once, as shown in this graph comparing Ashkenazi Jews to each other, where genomes 1, 3, 4, 5, 8, 9; genomes 2, 7; and genomes 6, 10, plainly form three distinct profiles.

The idea is you do this for every genome in a given population individually, and this will construct a dataset of vectors in the form of P, one for each genome in the population (i.e., a number of rows equal to the number of genomes, each row in the form of P, together forming a matrix with four columns). Note however, you’re comparing genomes to other genomes in the same population (e.g., German mtDNA compared to German mtDNA). You then do this for every population, separately, constructing unique matrices for each population (i.e., one matrix for German, Italian, etc.).

Now combine all of the matrices into a single matrix dataset, and treat the known classifiers as unknown, and try to predict the classifier of a given profile (in this case nationality, e.g., German).

Simply run Nearest Neighbor, mapping to , for which the Euclidean norm of the difference is minimum, treating the classifier of as the predicted classifier of . You’ve now converted DNA into a real number dataset, with just 4 columns, as opposed to a full genome, which in this case consists of about 17,000 columns.

I did exactly this over a dataset of 172 full genomes, from 18 populations, and the accuracy was 82.56%, without any other refinement. The total runtime was just 0.390 seconds, running on a MacBook Air. There is no way you’ll achieve this kind of runtime using Neural Networks. Each of the populations has only 10 full genomes, suggesting higher accuracy could be possible by simply increasing the size of the dataset. Other techniques can likely also improve accuracy.

Because mtDNA is inherited directly from the maternal line, if it weren’t for mutations, a perfect copy would be passed on from mother to daughter, etc, with the male line’s mtDNA simply vanishing. Nonetheless, we know that there is significant variation in mtDNA, which implies significant mutation. However, this work shows unambiguously that there is local variation, in that people that occupy the same present geographies, have similar mtDNA. This simply doesn’t make sense, unless there is some environmental impact on the mutations on mtDNA, causing people in similar environments to have similar mutations.

I think instead, it’s far more reasonable to assume that the male line actually does impact mtDNA indirectly, through the genetic machinery, which must be at least partly inherited from the paternal line. That is, the mechanisms that read and replicate DNA, and produce proteins, are not to my knowledge inherited from either sex exclusively. This implies that common paternal lines could produce similar mutations, which would explain the local similarity of mtDNA, and still allow for mutation. This implies that the paternal line could be discoverable through mtDNA alone, through the analysis of similar mutations on the same maternal line. For the same reasons, it implies that people with highly similar mtDNA would have similar paternal and maternal lines.

Here’s the dataset:

https://www.dropbox.com/s/mj8qk8jxybc9wbc/MTDNA.txt?dl=0

Here’s the code:

https://www.dropbox.com/s/y59ezd50k8df2sa/Build_Class_Profiles_CMNDLINE.m?dl=0
https://www.dropbox.com/s/e07o4x9fhlwxo2d/NN_fully_vectorized_BlackTree.m?dl=0
https://www.dropbox.com/s/b5d19n63q9q85zh/Genetic_Nearest_Neighbor_Single_Row.m?dl=0

THIS WAS THE RESULT OF BAD DATA, DISREGARD. THE ALGORITHMS ARE HOWEVER GOOD IN CONCEPT.

I’ve assembled a dataset using complete mtDNA genomes from the NIH, for 10 individuals that are Kazakh, Nepalese, Iberian Roma, Japanese, and Italian, for a total of 50 complete mtDNA genomes. Using Nearest Neighbor alone on the raw sequence data, the accuracy is about 80%, and basic filtering by simply counting the number of matching bases brings the accuracy up to 100%. This is empirical evidence for the claim that heritage can be predicted using mtDNA alone. One interesting result, that could simply be bad data, the Japanese population (classifier 4 in the dataset), contains three anomalous genomes, that have an extremely low number of matching bases with their Nearest Neighbors. However, what’s truly bizarre, is that whether or not you include these individuals in the dataset (the attached code contains a segment that removes them), generating clusters using matching bases suggests an affinity between Japanese and Italian mtDNA. This could be known, but this struck me as very strange. Note that because matching bases is plainly indicative of common heritage, this simply cannot be dismissed.

 

The chart on the left shows accuracy as a function of confidence, which in this case is simply the number of matching bases between an input and its Nearest Neighbor. Note the x-axis on the left does not show the number of matching bases, and instead shows the ordinal index of the number of matches (i.e., a x value of 25 is the maximum number of matching bases, which is approximately 17,000). The chart on the right shows the distribution of classes in the clusters for the Japanese genomes, after removing the three anomalous genomes. Clusters are generated by fixing a minimum number of matching bases, in this case it’s fixed to the minimum match count for all Japanese genomes and their respective Nearest Neighbors. Any other genome that meets or exceeds this minimum is then included in the cluster for a given genome. Note the totals can exceed the size of the dataset, since the clusters are not mutually exclusive, and so e.g., the clusters for two Japanese genomes can overlap, adding to the total count using the same genomes. As you can see, it shows a strong affinity between Japanese and Italian mtDNA. The analogous chart for the Italian population shows a similar affinity for Japanese mtDNA. No other groups show any comparable affinity for Japanese mtDNA. Because DNA is finite, and e.g., mtDNA has a well-defined sequence length, the number of possible sequences is fixed. As a consequence, as you increase the minimum number of matching bases required for inclusion in a cluster, the number of possible sequences that satisfy that minimum decreases exponentially as a function of the minimum. Therefore, if you increase that minimum, groups that do not actually belong should drop off exponentially. Those that remain, at a rate that is not exponentially decaying are more likely to be bona fide members of the cluster.

Here’s the dataset, which you can expand upon by entering the following Query into the NIH Database:

“ddbj_embl_genbank[filter] AND txid9606[orgn:noexp] AND complete-genome[title] AND mitochondrion[filter]”

Here’s the code: