Common Ancestor for Global Maternal Line

November 17, 2025November 17, 2025 / erdosfan / Leave a comment

I’ve long suspected that the Phoenicians are the common ancestor of a lot of modern people in Northern Europe, parts of Africa, and East Asia. This is based on years of research at this point, but you can read this summary to get up to speed. I’ve finally developed a test that searches for the common maternal ancestor of the Tanzanians, the Basque, and the Koreans, and it turns out it’s still plausible that it’s the Phoenicians, but I’m starting to realize all of these tests simply tell me which population is the most ancient, without providing any obvious geography, which is what I’m really looking for. More to come, code below.

Common Ancestor Algorithm Download

Meaningful Mathematical Relationships

November 9, 2025November 10, 2025 / erdosfan / Leave a comment

I started thinking about correlation again, and it dawned on me, that when we do math and science, we’re looking for computable relationships between sets of numbers. The most basic example is a function that describes the behavior of a system. Ideally, we have exact descriptions, but we often settle for probabilistic descriptions, or descriptions that are exact within some tolerance. I’d say that the search for computable relationships between sets of numbers is in fact science. But when you consider the full set of relationships between two sets of numbers, the set we’re interested in is therefore minuscule in terms of its density. In the extreme case, the set of computable functions has a density of zero compared to the set of non-computable functions. Yet, science and mathematics have come to the point where we can describe the behaviors of far away worlds, and nanoscopic terrestrial systems.

Therefore, it’s tempting to think that the computable is everything, and the balance of relationships are nonsense. For physical intuition, consider a Picasso painting represented as an RGB image, and compare that to the full set of random RGB images of the same size. What’s strange, is that the set in question will contain other known masterpieces, and new unknown masterpieces, if the image is large enough and the pixel size is small enough. And while I haven’t done the math, I’d wager the density of masterpieces is quite small, otherwise we’d all be famous painters, and since we’re not, I don’t think you can gamble your way into a masterpiece.

Similarly, if I have two sets of random numbers, and I simply connect them with strings, you’d probably think I’m a lunatic, though I’ve just defined a function. Whereas if I point out that I can inject the set of integers into the set of even integers, you’d swear I’m a genius. This might seem like unscientific thinking, but it isn’t. It’s arguably all the same, in that humans have a clear preference for computability, and that translates into a preference for symmetry over asymmetry. Personally, I listen to a lot of strange, highly random music, and enjoy Gregory Chaitin’s work as well, but in all seriousness, are we missing valuable information in the form of more complex functions, and perhaps tragically in the form of non-computable functions, assuming no non-computable machine exists?

Halting Processes and Proofs

November 2, 2025November 3, 2025 / erdosfan / Leave a comment

I was again reading my absolute favorite book on mathematics, Mathematical Problems and Proofs [1] (no, I am not paid for this endorsement, it really is that great), and on page 11 of the text, Example 1.20 gives Euclid’s Theorem on Prime Numbers, demonstrating that the set of prime numbers must be infinite. I immediately recalled that all natural numbers are either prime, or the product of primes, known as the Fundamental Theorem of Arithmetic. This is a different result, the proof of which is not presented in [1] (at least I didn’t see it).

I checked Google, and there’s a straightforward proof using induction, but it lacks intuitive appeal. As such, I spent a few minutes this morning thinking about it, and I realized you can construct an intuitive proof. I haven’t seen this proof elsewhere, though it could be a known result. Even if it is known, what’s interesting is the structure of the proof, which is you can show that it must be the case that the algorithm upon which the proof relies, will eventually halt. This is pretty interesting, and maybe it’s a new form of proof. At a minimum, we have an intuitive proof of the Fundamental Theorem of Arithmetic that does not rely on induction.

The Proof

Assume you have a natural number $n \in \mathbb{N}$ . If $n$ is prime, then we’re done. So assume that $n$ is not prime. As such, it must be the case that $n = a_1b_1$ , for $a_1,b_1 \in \mathbb{N}$ , and therefore, $a_1 = \frac{n}{b_1} \in \mathbb{N}$ . The intermediate result will be to show that all numbers are either prime, or have at least one prime factor, which we will then use to prove the Fundamental Theorem of Arithmetic. 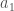As such, if $a_1$ is prime, then we’re done. Therefore, assume 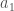$a_1$ is not prime, and as such, $a_2 = \frac{a_1}{b_2}$ , for $a_2,b_2 \in \mathbb{N}$ . We can of course continue to apply this process for increasing values of $i \in \mathbb{N}$ , generating decreasing values of $a_i$ . 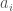However, there are only finitely many numbers less than 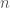$n$ , and as such, this process must eventually terminate, producing a prime number $a_m = \frac{a_{m-1}}{b_m}$ . Note that $a_m = \frac{n}{b_1 \cdots b_m}$ , and as such, $n = a_m (b_1 \cdots b_m)$ . Therefore, all natural numbers have at least one prime factor.

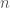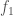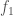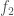Now let’s express $n$ as the product of this prime number $p_1 = a_m$ , and the remaining factors, $f_1 = b_1 \cdots b_m$ , i.e., $n = p_1f_1$ . Note that $f_1$ cannot be prime, so we can therefore run the algorithm above on $f_1$ , which will produce another prime number factor $p_2$ , and another remaining factor $f_2$ , such that $n = p_1p_2f_2$ . Note that it must be the case that $f_2 < f_1$ , and in general, $f_{i+1} < f_i$ , and therefore it requires fewer steps to calculate each successive prime factor. Because the number of steps is always a natural number, this process must terminate. 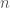Therefore, $n$ will eventually be expressed as the product of a finite number of primes.