Spatial Entropy

I noted on Twitter that I came up with a really efficient way of calculating spatial entropy, and though I plan on writing something more formal on the topic, as it’s related to information theory generally, I wanted to at least write a brief note on the method, which is as follows:

Let be a set of points in Euclidean -space. Sort them by row value, which will produce a sorted matrix of vectors . Now take the norm of the difference between all adjacent entries, , which will produce a vector of real numbers, that correspond to the norms of those differences. Let be the sum over the entries in the vector , and take the entropy of the vector , which will correspond to a distribution.

So for example, if you have points along a line, and all of them are equidistant from one another, then the entropy will be equal to the , which corresponds to a uniform distribution, which is consistent with intuition, since you’d expect entropy to be maximized. In contrast, if all points are at the same location, then their distances would be zero, and the entropy would be zero.

You could do the same with a set of curves, but you’d need a comparison operator to first sort the curves and then compare their distances, and for this, you can use the operators I used in Section 1.3 of my A.I. summary (the “Expanding Gas Dataset”).

This allows for the measurement of the the entropy of an arbitrary dataset of vectors.

Information, Knowledge, and Uncertainty

The fundamental observation I’ve made regarding uncertainty, is that what you know about a system plus what you don’t, is all there is to know about the system. This sounds tautological, but so is the founding equation of accounting, which was also founded by an Italian mathematician, which it seems clear people are trying to forget.

Expressed symbolically, the equation states that:

,

Where is the information content of the system, is your knowledge with respect to the system, and is your uncertainty with respect to the system. I go through some examples in this note on the matter, but the intuition should be straightforward.

Because we can now measure spatial entropy, we can measure the entropy of a dataset, which would also be the information content, , of the dataset, but let’s table that for a moment.

My prediction algorithms return a set of vectors given an input vector, and it allows for blank entries in the input vector. So if you observe the first 50 out of 1,000 states of a system, you’ll get a set of vectors that reflect the information you have, and of course, that set winnows down in size as the number of observations increases (see Section 3.1 of A New Model of Artificial Intelligence).

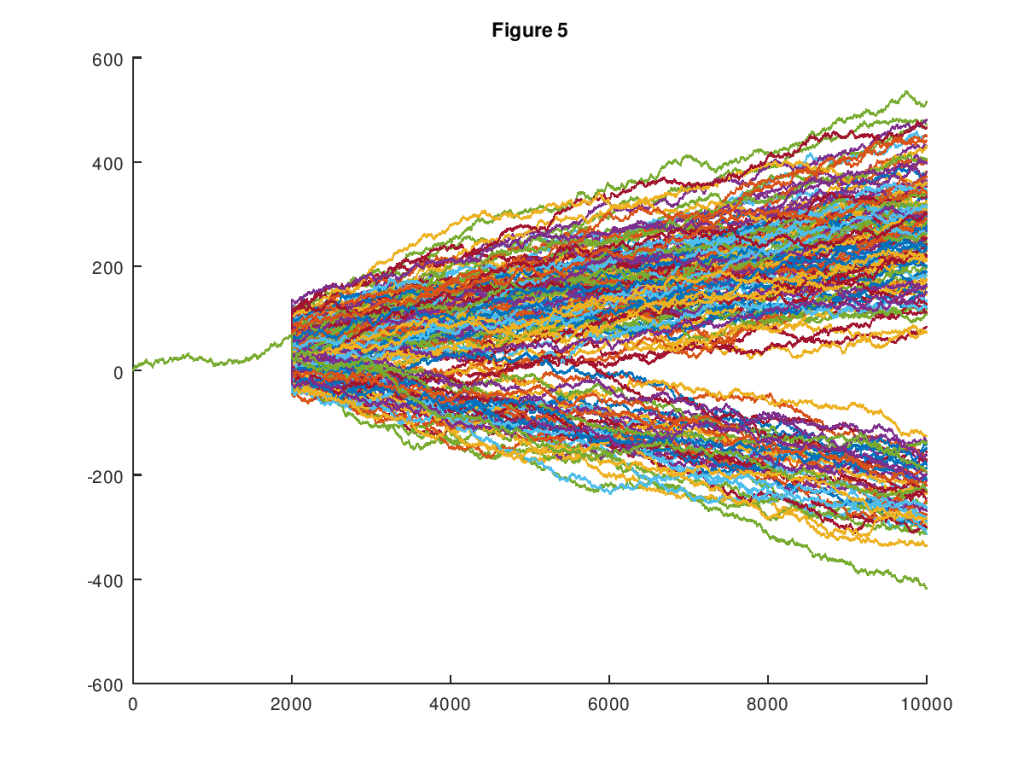
Here’s a representative chart (from that paper) that shows how the set of possible paths of a random walk starts to tilt in favor of an upward path as data becomes available. In this case, 2,000 observations are available out of 10,000, and the input vector is in fact an upward tilting path.

We can also measure the entropy of this set of returned set of predictions, using the same method described above, which would in my opinion represent your uncertainty with respect to your prediction. This makes sense, because in the worst case, you get back the full training dataset, which would set your uncertainty equal to the information content of the dataset.  Expressed symbolically,

.

This implies that your knowledge with respect to your prediction is zero, which is correct. That is, if your prediction algorithm says, my prediction is, the entire training dataset, then it doesn’t know anything at all. As observations become available, the set of returned predictions will shrink in size, which will reduce the entropy of the returned prediction set, implying non-zero knowledge. Eventually, you could be left with a single prediction, which would imply perfect knowledge, and no uncertainty, in the context of your training dataset, which is all you ever know about a given problem.